Nos dias de 29 e 30 de maio de 2019 ocorreu a oficina do PIBID Matemática na Escola Estadual de Ensino Médio São Caetano dentro do Rally Científico, proposto pela escola.
 |
| Bolsistas ensinando os alunos a calcularem o número de ouro. |
 | |
|
 | |
|
Conjuntos Numéricos
Os conjuntos numéricos foram criados com a ideia de organizar os números e suas propriedades em conjuntos.
Nas mais primitivas organizações sociais, as pessoas já se deparavam com a necessidade de registrar acontecimentos, fatos e quantidades. Assim, cada civilização criou símbolos que representassem palavras, situações e números.
A representação de quantidades tornava-se cada vez mais complexa, à medida que surgiam necessidades menos elementares. Por exemplo, a de conhecer a razão entre o comprimento e o diâmetro de uma circunferência.
Além disso, com os avanços no estudo da álgebra e dos processos de resolução de equações, era necessária uma sistematização e organização dos números em grupos (ou conjuntos). Desse modo, foram criados conjuntos numéricos.
O que são conjuntos numéricos?
Um conjunto é a união de elementos que possuem atributos semelhantes. Os conjuntos numéricos são a união de números que possuem as mesmas características.
Conjunto dos números naturais
Os números naturais são números inteiros e positivos, incluindo o zero. O conjunto dos números naturais é representado por N.
N= {0, 1, 2, 3, 4…}
Conjunto dos números inteiros
Os números inteiros são representados pela letra Z. Esse conjunto contempla todos os números naturais e também os números negativos.
Z= {… -4, -3, -2,-1, 0, 1, 2, 3, 4…}
Conjunto dos números racionais
Os números racionais ou conjunto dos quocientes entre dois número inteiros são todos aqueles que podem ser representados em uma razão.
O numerador e denominador precisam ser números inteiros e diferentes de zero. Esse conjunto é representado pela letra Q.
Além de frações, os números racionais podem ser escritos em decimal finita (0,3; 1,25) ou infinita periódica (0,333..). Os números naturais e inteiros são subconjuntos dos número racionais.
Conjunto dos números irracionais
Os números irracionais, representados pela letra I, são aqueles que não podem ser obtidos pela divisão de dois números inteiros sendo decimais infinitos e não periódicos. Ou seja, não tem repetições nas casas decimais. São os chamados decimais não exatos, como 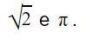
Esse conjunto é representado pela letra R e engloba todos os números racionais e irracionais. Os números racionais e irracionais não possuem elementos em comum. Cada um pertence a um conjunto distinto. Por esse motivo, foi necessária a criação de um conjunto que unisse os dois.
Número de ouro 
Entre os números irracionais existem alguns que vocês conhecem, o PI por exemplo e hoje vamos falar sobre um outro irracional conhecido, o Phi.
Conhecido também como número de ouro, Phi representa a pronúncia da letra f em grego, inicial do nome Fídeas, um arquiteto e escultor grego que construiu Partenon, em Atenas. Em decorrência das suas inúmeras aplicações, ele passou a ser considerado por muitos como uma oferta de Deus ao mundo, cuja simbologia é Φ.
A representação numérica do número de ouro pode ser constatada a partir da razão 1+√5/2, que resulta na dízima não periódica 1,61803398… De tal modo que Φ equivale a um termo irracional, obtido por meio da razão áurea; A aplicação do número de ouro se dá desde os primórdios. As pirâmides de Gizé, no Egito Antigo, por exemplo, foram erguidas tendo por base tal razão numérica: A razão entre a altura de uma face e a metade do lado da base da pirâmide maior é igual ao termo de ouro. Edificado entre 447 e 433 a. C., o templo de Partenon tem presente no retângulo da sua fachada a proporção de ouro (largura/altura). Os pitagóricos também fizeram uso da razão áurea na estrela pentagonal.
Além do matemático grego Endoxus, que a partir dos seus estudos pesquisou sobre a secção que se entende ser a secção áurea. Por fim, vale menção também a aplicação da razão áurea por Fibonacci quando descreveu uma população de coelhos em 1202. A aplicação do número de ouro tem inúmeras finalidades, sendo impossível determinar uma quantidade exata do emprego dessa razão. O termo f pode ser constatado em plantas diversas, como as flores, além de em triângulos e retângulos. Ainda é possível constatar tal razão em obras de arte, construções, em elementos naturais diversos e há quem diga que até em outras matérias que o homem ainda não teria descoberto.
O número de ouro e o corpo humano
A seguir algumas partes da anatomia humana onde podemos encontrar a proporção áurea.
Em destaque na imagem abaixo a mão humana e suas medidas proporcionais.
Além disso, podemos considerar:
- A altura do corpo humano e a medida do umbigo até o chão.x ( MÉDIA ARITMÉTICA DE TODAS AS MEDIDAS)
- A altura do crânio e a medida da mandíbula até o alto da cabeça.
- A medida da cintura até o queixo e o tamanho do tórax.
- A medida do ombro à ponta do dedo e a medida do cotovelo à ponta do dedo.
- O tamanho dos dedos e a medida da dobra central até a ponta.
- A medida da dobra central até a ponta dividido e da segunda dobra até a ponta (não)
- A medida do seu quadril ao chão e a medida do seu joelho até ao chão.
Essas proporções anatômicas foram bem representadas pelo "Homem Vitruviano", obra de Leonardo Da Vinci. O Homem Vitruviano é um desenho famoso que acompanhava as notas que Leonardo da Vinci fez ao redor do ano 1490 num dos seus diários. Descreve uma figura masculina desnuda separadamente e simultaneamente em duas posições sobrepostas com os braços inscritos num círculo e num quadrado. A cabeça é calculada como sendo um oitavo da altura total. Às vezes, o desenho e o texto são chamados de Cânone das Proporções.
O desenho atualmente faz parte da coleção/coleção da Gallerie dell'Accademia (Galeria da Academia) em Veneza, Itália.
O Homem Vitruviano é baseado numa famosa passagem do arquiteto/arquiteto romano Marcus Vitruvius Pollio na sua série de dez livros intitulados de De Architectura, um tratado de arquitetura em que, no terceiro livro, ele descreve as proporções do corpo humano:
Bolsistas: Micael Brambilla Pellizzer, Simone Araldi, Natália Bolfe, Vanessa Novello ( quem mais foi dia 29 e 30?)
Escola atendida: Escola Estadual de Ensino Médio São Caetano.
Séries atendidas: Ensino Médio
Professora Orientadora Ana Cristina Possapp Cesa
Professora Supervisora Silvana Roseli Contini da Rosa e Léia Ribeiro.
Apoio - CAPES - Programa Pibid

Nenhum comentário:
Postar um comentário